最近看到好多有關計算有效質量的帖子。在論壇內搜了下,發現很多都側重于軟件具體操作,而對單位準換等細節問題講述的較少。因此鄙人結合自己對有效質量的理解,闡述下自己想到的一種計算有效質量的方法。不足之處,還望多多指正。
有效質量的表達式,一般固體物理教材上都有:
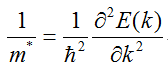
在帶入物理量進行計算時,涉及單位制問題。一般寫輸入文件時,長度單位為埃;而程序輸出的能帶結構中,能量單位為eV(abinit是個例外,默認輸出能量單位為hartree)。這兩個單位實際上是國際單位制下的單位,在此單位制下計算不僅要查找約化普朗克常數h_bar的值,最后算得有效質量單位為千克,還得換算成電子質量倍數,非常麻煩。而改用原子單位制就可省去這些步驟。因此算有效質量第一步就是將所有物理量轉換成原子單位制。
原子單位制有兩種,一種為Hartree原子單位制,另一種為Rydberg單位制。這兩種單位制的區別在于,Hartree單位制下基本物理量簡單,電子電荷和質量都為1;而Rydberg單位制下薛定諤方程簡單,系數為1。由于Rydberg單位制下電子質量定義為1/2,這不太符合一般認知規律(就像某些編程語言中從0開始的數組下標一樣,扯遠了),因此一般轉換成Hartree單位制。Hartree單位制下,一長度單位等于1bohr等于0.52917721092埃,一能量單位等于27.21138506eV,約化普朗克常數值為1。這樣有效質量表達式中的約化普朗克常數就沒了。
第二步,是根據原胞基矢和正倒格子基矢間對應關系,算出倒格子基矢。
以單層二硫化鉬為例,其為六方晶系,原胞基矢長度為3.20埃,c軸設定為10埃。在以埃為單位長度的笛卡爾坐標下,三個正格子基矢的坐標為:
a1 = 1.600000000 2.771281292 0.000000000
a2 = -1.600000000 2.771281292 0.000000000
a3 = 0.000000000 0.000000000 10.000000000
實際上正格子基矢在笛卡爾坐標系中有無數種擺法,這里選取了其中一種,讓a1,a2對稱分布在y軸兩側。
將坐標轉換成原子單位制:
a1 = 3.023561799 5.236962656 0.000000000
a2 = -3.023561799 5.236962656 0.000000000
a3 = 0.000000000 0.000000000 18.897261246
再根據公式:
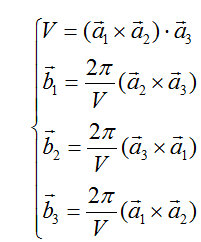
算得倒格子基矢坐標為:
b1 = 1.039037024 0.599888305 -0.000000000
b2 = -1.039037024 0.599888305 0.000000000
b3 = 0.000000000 -0.000000000 0.332491848
對于六角晶系,如果正格子基矢夾角為60度,倒格子則為120度。
取一條K路徑:
G: (0, 0, 0) # Gamma
M: (1/2, 0, 0)
K: (2/3, 1/3, 0)
以上各K點坐標為分數坐標,換算成笛卡爾坐標:
G: ( 0, 0, 0 )
M: ( 0.5195185, 0.2999442, 0.0 )
K: ( 0.3463457, 0.5998883, 0.0 )
各K點間距:
|GM| = 0.5998883 bohr^-1, |MK| = 0.3463456 bohr^-1, |KG| = 0.6926914 bohr^-1。
在計算能帶時各高對稱點間均勻撒點。按圖中方法確定從出發點到當前點所走過的路徑長度,最為自變量x:
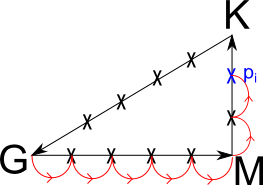
將能量轉換成以Hartree為單位后,作為y。
定位價帶頂和導帶底,對那一段進行多項式擬合,得到y與x的表達式(實際上是E與k的表達式)。
將y對x求二階導數,計算在價帶頂和導帶底的導數值(如果用二次函數擬合,二階導數應該為常數),再取其導數,即有效質量。
此有效質量單位是電子質量。例如結果是0.5,則表示有效質量為電子質量0.5倍。
最后附帶一個由正格子基矢算倒格子基矢的python腳本
http://emuch.net/bbs/viewthread.php?tid=7149817&fpage=1
|