這是我的答案(雖然我看不懂)
無論是積分和微分,都有符號和數值兩種操作,符號操作是計算精確解析式和相應的精確值: 符號: sysm x t---->定義自變量 int(f,x) ---->求f關于x的不定積分 int(g,t) ---->求g關于t的不定積分 int(f,x,a,b) ---->求f關于x在[a,b]上的定積分 diff(f,x,n) ---->求f關于x的n階導數
數值方法: 數值微分: #用函數值的差分除以自變量的差分(只要步長足夠小,就足夠精確) diff(y). /diff(x),但是會比原函數的維度少一位 數值積分: #數值積分可以基于不同的積分準則,如:中點法則、梯形法則、辛普森法則等,因此也有不同的函數 1. 基于自適應 Simpson 積分法計算數值積分(不推薦) 如:計算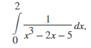 ,可以: ,可以: 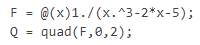 ,F為待計算函數句柄(匿名) ,F為待計算函數句柄(匿名)2. 基于自適應Gauss-Lobatto方法(不推薦) 和quad一樣的用法,把quad換成quadl 3. 基于高斯-勒讓德積分方法(和integral的積分方法基本相同) 和quad一樣的用法,把quad換成quadgk 4. 基于全局自適應積分法(推薦) 與quad一樣的用法,將quad換成integral 5. 基于梯形積分法 
- %研究各種信號的抗噪聲性能(直接引用前幾個文件的基礎代碼)
- clear all;
- close all;
- %tips: biterr函數、randn函數
- %-------------------------ASK---------------------------
- %----原始信號碼元參數----
- Tb = 1; %碼元長度
- fs = 100; %采樣頻率
- dt = 1/fs; %采樣時間間隔
- N = 1e5; %碼元數量,數量大,便于統計,避免較少的碼元數帶來的偶然性
- t = 0:dt:(N*fs-1)*dt; %時域范圍
- %----載波參數----
- Ac = 1; %載波幅度
- fc = 30; %載波頻率
- phi = 0; %初始相位
- %----產生原始的二進制碼元----
- sr = (sign(randn(1,N))+1)/2; %原始信息序列
- sr_conv = zeropad(sr,fs);
- nrz = ones(1,fs); %單個NRZ波形
- data = conv(sr_conv,nrz);
- data = data(1:length(t));
- %----產生ASK信號----
- carrier = cos(2*pi*fc*t);
- ask = data.*carrier;
-
- %----匹配濾波----
- r_db = 0:15; %信噪比-dB
- Eb = Tb*Ac*Ac/2; %單個比特的信號功率(J/bit)
- pe = zeros(1,length(r_db));
- pe_ideal = zeros(1,length(r_db));
- for i=1:length(r_db)
- r = 10^(r_db(i)/10);
- n0 = Eb/r; %單邊噪聲功率譜密度
- delta = n0/2*fs; %噪聲功率
- n = sqrt(delta)*randn(1,length(ask)); %噪聲信號
- % reciv = awgn(ask,r_db(i)); %也可以這樣
- reciv = ask+n; %接收信號
-
- %匹配濾波器
- t1 = 0:dt:Tb-dt;
- h = cos(2*pi*fc*t1);
-
- %濾波
- recov_signal = conv(reciv,h)*dt;
-
- %包絡檢波
- t2 = 0:dt:(length(recov_signal)-1)*dt;
- z = hilbert(recov_signal); %z為解析信號
- z1 = z.*exp(-sqrt(-1)*2*pi*fc*t2); %z1為復包絡
- envlp = abs(z1);
- % subplot(2,1,1);
- % plot(t,data);
- % subplot(2,1,2);
- % plot(t2,recov_signal);
-
- %判決
- recov_sym = zeros(1,N);
- Vth = Ac/4; %判決門限,余弦信號卷積之后,高度會下降一半,故用Ac/4
- for j=1:N
- if envlp(j*Tb/dt) > Vth
- recov_sym(j)=1;
- else
- recov_sym(j)=0;
- end
- end
- [err_num,err_pro] = biterr(sr,recov_sym); %計算誤碼個數和誤碼率
- pe(i)=err_pro;
- pe_ideal(i) = 0.5*erfc(sqrt(0.25*r));
- %pe_ideal(i) = 0.5*exp(-0.25*r);
- end
- figure();
- semilogy(r_db,pe,'-*');
- hold on;
- semilogy(r_db,pe_ideal);
- legend('實際誤碼率','理論誤碼率');
- grid on;
- % 評估二進制單極性和雙極性基帶系統的抗噪性能
- SNR_dB = 0:0.05:10;
- scal = 10.^(SNR_dB/10); %信噪比的比例形式
- A_over_sigma = sqrt(scal)*sqrt(2);
- double = 0.5*erfc(sqrt(scal));
- single = 0.5*erfc(0.5*sqrt(scal));
- figure('NumberTitle', 'off', 'Name','相同抽樣電平下兩種數字基帶系統的抗噪聲能力');
- semilogy(A_over_sigma,double);
- hold on;
- semilogy(A_over_sigma,single);
- xlabel('抽樣電平/噪聲均方值');
- ylabel('系統誤碼率Pe');
- grid on;
- legend('雙極性','單極性');
- %tips:數字基帶系統的抗噪性能(不考慮碼間干擾,受噪聲引起的誤碼率)與信號碼元抽樣電平的值與噪聲均方根值(功率開方,即高斯噪聲的方差開方)之比有關
- %如果是理想的方波碼元,功率為A
- %第4-5行其實是驗證了兩種編碼方式:相同的電平值A和噪聲均方值下不同的抗噪表現,而不是相同的信噪比條件下,因為如果兩個信號的SNR相同,則兩個信號的電平值也不同
- %----驗證相同SNR下不同系統的抗噪性能(此時兩種信號的電平值也不同)-----
- double_2 = 0.5*erfc(sqrt(scal)/sqrt(2));
- single_2 = 0.5*erfc(sqrt(scal)/2);
- figure('NumberTitle', 'off', 'Name','相同SNR下兩種數字基帶系統的抗噪聲能力');
- semilogy(SNR_dB,double_2);
- hold on;
- semilogy(SNR_dB,single_2);
- xlabel('SNR(Eb/N0)-dB');
- ylabel('系統誤碼率Pe');
- grid on;
- legend('雙極性','單極性');
代碼下載:
 Communication-Matlab-main.7z
(71.93 KB, 下載次數: 0)
Communication-Matlab-main.7z
(71.93 KB, 下載次數: 0)
2025-6-13 18:48 上傳
點擊文件名下載附件
通信原理answer 下載積分: 黑幣 -5
|