倒立擺是一個典型的多變量、非線性、強耦合、欠驅動的自然不穩定系統,對倒立擺系統的控制研究,能反映控制過程中的鎮定、非線性和隨動等問題,因此常用于各種控制算法的研究。
本次課設我以直線二級倒立擺系統為模型,闡釋了直線二級倒立擺的建模方法和鎮定控制算法。其次介紹了直線二級倒立擺系統的結構和參數,應用拉格朗日方程建模方法詳細推導了二級倒立擺的數學模型,并對系統的性能進行分析。接下來,本文重點研究了最優控制算法在直線二級倒立擺鎮定控制中的應用;在介紹倒立擺系統的最優控制算法的基礎上,設計了系統的最優控制器,分析得出控制參數的選擇規律;并且在Simulink上完成仿真實驗,觀察控制系統性能。
倒立擺是進行控制理論研究的典型實驗平臺,許多抽象的控制理論概念,如系統的穩定性、可觀性及可控性等都可以通過該系統直觀地表示出來。因此,近幾年來,該系統已經成為控制領域的研究熱點。 倒立擺系統是一個典型的非線性、強耦合、多變量和不穩定系統。在控制研究領域有著代表性的意義。倒立擺作為控制系統的被控對象,許多抽象的控制概念都可以通過它直觀的表現出來。本次課設我選用以二級倒立擺為研究對象,采用牛頓力學定律進行數學建模,利用二次型最優控制器( LQR)求出最優狀態反饋矩陣K,經過對Q和R兩個加權矩陣的選取實現二級倒立擺的自動控制。該方法為多變量反饋系統的設計提供了有效的分析法,可適于時變系統,處理擾動信號和測量噪聲,處理有限和無限的時間區間。
1 系統建模 1.1相關數據 為簡化系統,我們在建模時忽略了空氣阻力和各種摩擦,并認為擺桿為剛體。 二級倒立擺的組成如圖 1 所示: 圖 1 直線兩級倒立擺物理模型 首先,對該系統做如下假設: 1)小車、一級擺桿和二級擺桿都是剛體。 2)皮帶輪與同步帶之間無相對滑動,且同步帶不會拉伸變長。 3)小車與導軌之間的摩擦力與小車速度成正比。 4)各級擺桿與轉軸間的轉動摩擦力矩與擺桿的角速度成正比。 表1 二級倒立擺各物理參數:
1.2理論依據 1.2.1 受力分析 利用拉格朗日方程推導運動學方程: 拉格朗日方程為: 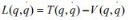 (1-1) 其中 L 為拉格朗日算子,q 為系統的廣義坐標,T 為系統的動能,V 為系統的 勢能。 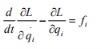 (1-2) 其中 i=1,2,3……n, i f 為系統在第 i 個廣義坐標上的外力,在二級倒立擺系統中,系統的廣義坐標有三個廣義坐標,分別為 x, θ1, θ2 。 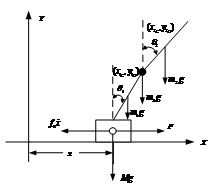
圖2 直線二級倒立擺受力分析 先對倒立擺的物理模型進行分析,如圖2所示,然后建立擺桿和質量塊的質心的坐標表達式。這里規定擺桿1的質心坐標為 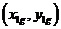 ,擺桿2的質心坐標為 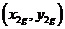 ,質量塊的質心坐標為 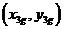 。質心坐標如下: 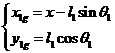
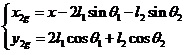 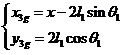
在直線二級倒立擺系統中,廣義坐標為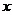 , ,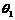 和 和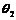 。根據倒立擺的物理模型分析圖,列寫出系統的動能為: 。根據倒立擺的物理模型分析圖,列寫出系統的動能為: 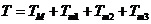 (1-3) (1-3) 其中, 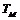 、 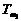 、 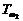 和 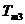 分別為小車、擺桿1、擺桿2和質量塊1的動能,它們分別為: 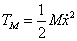 (1-4) 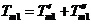 (1-5) 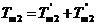 (1-6) 其中, 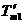 和 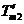 分別為擺桿1和擺桿2質心平動動能, 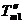 和 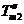 分別為擺桿1和擺桿2繞質心轉動動能。然后,應用擺桿和質量塊質心表達式求出系統的動能。 將質心坐標帶入公式(1-6)擺桿1的動能為: 所以得到 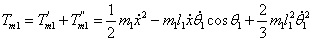 (1-7) 同理帶入(1-7),求出擺桿2的動能為: 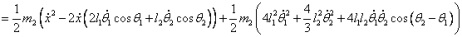 (1-8) 同理帶入(1-5),質量塊1的動能為: 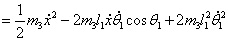 (1-9) 因此將(1-7)(1-8)(1-9)帶入(1-3),可以得到系統動能為 另一方面,系統的勢能為 從而得到Lagrange函數為 1.2.2 列出Lagrange方程 由于在廣義坐標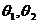 上均無外力作用,故列寫Lagrange方程得到 上均無外力作用,故列寫Lagrange方程得到 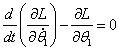 (2-1) 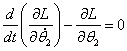 (2-2) 將L代入式(2-1)和(2-2)得到 上述方程為倒立擺的動力學方程,求解微分方程可以得到倒立擺狀態量 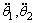 的表達式,然后可以建立倒立擺的數學模型。
1.3 倒立擺運動方程的線性化處理 針對已建立的拉格朗日方程,求解方程可以得到倒立擺狀態量 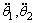 的表達式。由于 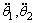 是關于系統的狀態變量和輸入控制量u的方程,小車施加的加速度信號作為控制量,有 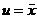 ;因此設方程的解為: 對倒立擺模型進行線性化處理,這里采用在平衡點附近將函數進行泰勒級數展開。上面的方程為七元函數,因此采用對多元函數展開的方法展開,這里對二元函數的泰勒級數展開方法進行介紹。 二元函數的形式為 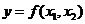 ,在其平衡點 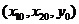 附近進行泰勒級數展開。在平衡點附近,由于偏差 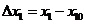 及 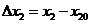 的絕對值很小,可以省略函數高次項得: 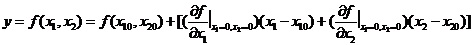 (3-1) 將上式化簡,得到一次線性方程: 這樣, 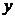 與 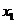 和 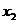 之間的非線性關系,轉化為 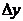 與 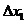 和 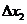 之間的線性關系。當系統的平衡點處于原點時,即 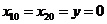 ,可以對方程化簡為: 按照二元函數的泰勒級數展開方法對公式(3-1)進行展開,由于直線二級倒立擺系統的平衡點為: 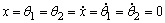 ;因此線性化后得到 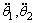 的表達式為: 其中 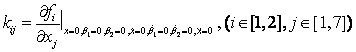 由于求解微分方程比較繁瑣,因此對線性化處理后的方程采用mathematica軟件編寫程序,求解倒立擺狀態量 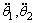 的表達式。根據得到的參數,建立倒立擺的數學模型。
運行程序求出倒立擺狀態量 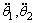 的表達參數 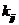 ,其中k11、k14、k15、k16、k21、k24、k25、k26的值為0,其余各參數的表達式如下: (g取10N/kg,M=1.32kg,m1=0.04kg ,m2=0.132kg,m3=0.208kg,l1=0.09m,l2=0.27m) 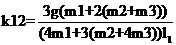 =78.64; 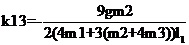 =-21.62; 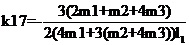 =5.70; 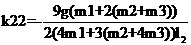 =-39.32; 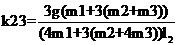 =38.59; 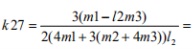 -0.029; 對二級倒立擺系統,取系統狀態變量為 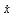 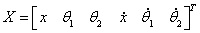 [1],然后建立連續狀態空間方程為: 根據系統狀態變量直接的關系,寫出系統的狀態空間方程為:
1.4 能控能觀性檢測 1.4.1能控性檢測 QC=rank[B A*B A^2*B A^3*B A^3*B A^4*B]=6=n 完全能控 1.4.2觀測性檢測 UO=rank[C A*C A^2*C A^3*C A^3*C A^4*C]=6=n 完全能觀
2 模糊控制器的設計 2.1模糊控制器基本原理 模糊控制是以模糊集理論、模糊語言變量和模糊邏輯推理為基礎的一種智能控制方法,它是從行為上模仿人的模糊推理和決策過程的一種智能控制方法。該方法首先將操作人員或專家經驗編成模糊規則,然后將來自傳感器的實時信號模糊化,將模糊化后的信號作為模糊規則的輸入,完成模糊推理,將推理后得到的輸出量加到執行器上。 簡言之,模糊控制器會將輸入的誤差和誤差變化量的精確值進行模糊化,然后將模糊值進行邏輯推理,最后將得到的模糊值去模糊化再送出。 模糊控制器的結構如圖3所示。控制器由4個基本部分組成,即模糊化接口、知識庫、推理機、解模糊接口。 根據前面介紹的二級倒立擺穩定控制思想,采用融合技術設計一個線性融合函數,把多個變量融合成為綜合誤差E和綜合誤差變化率EC,這就可以使模糊控制器的設計大為簡化。如圖4。 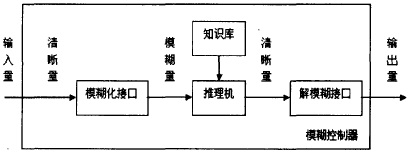
圖3模糊控制器的結構 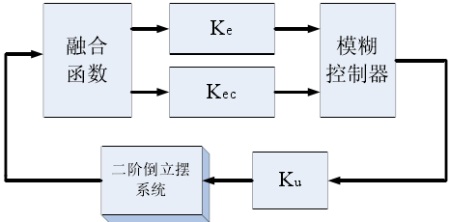
圖4 采用融合技術的模糊控制器 2.2模糊控制器設計步驟 (1)確定模糊控制器的輸入變量和輸出變量(即控制量); (2)設計模糊控制器的控制規則; (3)進行模糊化和解模糊化; (4)選擇模糊控制器的輸入變量及輸出變量的論域,并確定模糊控制器的參數(如量化因子、比例因子); (5)編制模糊控制算法的應用程序; 2.3模糊規則表

51hei.png (7.96 KB, 下載次數: 52)
下載附件
2021-5-16 19:34 上傳
If EC=NB and E=NB then U=NB ; If EC=NB and E=NM then U=NB If EC=NB and E=NS then U=NB If EC=NB and E=ZE then U=NM If EC=NB and E=PS then U=NM If EC=NB and E=PM then U=NS If EC=NM and E=NB then U=NB …… 2.4利用融合函數設計 基于LQR理論來為二級倒立擺的狀態方程設計一個狀態反饋矩陣K和降維矩陣G,將六個狀態變量綜合成兩個變量,即綜合誤差E和綜合誤差變化率EC。并通過LQR仿真,得出輸入輸出數據對,根據得出的數據,計算并制定出模糊規則。 利用最優控制理論計算出一組可以讓二級倒立擺穩定的狀態反饋矩陣K: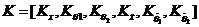 (2-1) (2-1) 最優控制性能指標函數為: 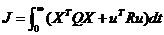 (2-2) (2-2)
通過使性能指標函數式(6-1)為最小,可求得: 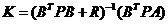 (2-3) (2-3)
求解如下Ricatti方程可得到矩陣P。 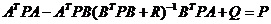 (2-4) (2-4)
性能指標函數中,矩陣Q和矩陣R這兩個參數需要定義,是用來平衡系統對輸入量和狀態量的敏感程度的。它們對閉環系統的動態性能影響很大。在倒立擺系統中,Q,R分別用來對狀態向量X和輸入控制量u進行平衡加權的。一般情況下,R增加時,控制力減小,角度變化變小,跟隨速度變慢。而Q中某元素增加時,其對應的狀態變量的響應速度增加,其它狀態變量的響應速度相對減慢。為了使得反饋矩陣K更合理,對矩陣Q, R的選取一定要盡量恰當。通過反復的測試,在實際系統的控制過程中,選取 
基于MATLAB強大的矩陣運算以及它豐富的內部函數,利用K=lqr(A,B,Q,R)命令通過計算,可得到狀態反饋矩陣K: K=[17.3205,111.7009,-200.6791,18.6848, 2.6899,-32.5784] 本文應用歸一化思想設計降維矩陣G。從上面的結論中得知狀態矩陣K中包含六個元素,分別代表著六個狀態變量的權值。根據歸一化思想,每個元素均除以矩陣K的范數,為了把六個狀態變量合并成兩個變量,設計如式(2-5 )形式的矩陣,利用狀態反饋陣K構造出降維矩陣G: 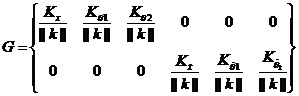 (2-5) (2-5)
其中,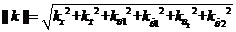 把所得狀態反饋陣K的值代入式(6-5 )得到G: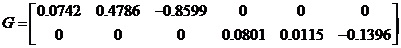 最后,通過降維矩陣G把六個狀態變量X綜合為兩個變量,稱為綜合誤差E和綜合誤差變化率EC。 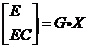 (2-6) (2-6)
2.5模糊控制器的輸入輸出論域及模糊集合的劃分 首先對系統進行采樣,粗略確定輸入輸出論域:位置[-0.2,0.2],速度[-1,1],下擺角[-0.15,0.15],下擺角速度[-4 , 4]上擺角[-0.08, 0.08],上擺角速度[-0.8, 0.8],控制力[-45,45]。為簡化,綜合誤差E、綜合誤差變化域EC和輸出量化域均為[-3,3]。 可大致估算E的量化因子為14,EC的量化因子為18,U的的比例因子為15。
3 matlab仿真 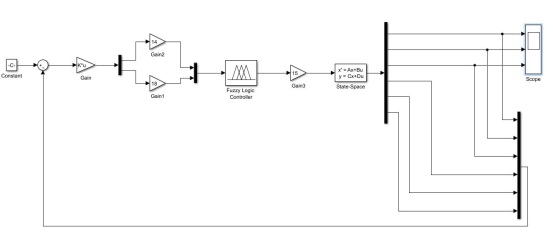
圖5 模型建立 該模型Constant初值我設定為0,融合矩陣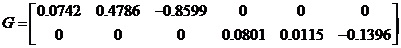 ,系統矩陣A= ,系統矩陣A= ,輸入矩陣B= ,輸入矩陣B=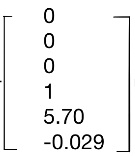 , , 輸出矩陣C= ,直聯矩陣D= ,直聯矩陣D= 。初始,我選定E的量化因子為14,EC的量化因子為18,U的的比例因子為15。 。初始,我選定E的量化因子為14,EC的量化因子為18,U的的比例因子為15。
圖5.誤差E 圖6.誤差率EC 圖7.模糊控制對應規則 (規則詳參) 表3 模糊規則表
If EC=NB and E=NB then U=NB ; If EC=NB and E=NM then U=NB If EC=NB and E=NS then U=NB If EC=NB and E=ZE then U=NM If EC=NB and E=PS then U=NM If EC=NB and E=PM then U=NS If EC=NM and E=NB then U=NB …… 圖8 仿真波形(E的量化因子ke為14,EC的量化因子kec為18,U的的比例因子ku為15) 通過波形可以清楚的看到,在選取E的量化因子為14,EC的量化因子為18,U的的比例因子為15后,整個倒立擺系統大概在2秒鐘略多一點,不到三秒鐘的時候達到穩定狀態,即兩桿豎直倒立不動,小車不再有位移。
圖8 仿真波形(E的量化因子ke為14,EC的量化因子為18,ku的的比例因子為20) 仔細觀察仿真波形圖,可以看到,比例因子增大,整個系統達到穩定的時間變長了。  圖9 仿真波形(E的量化因子ke為10,EC的量化因子kec為18,U的的比例因子ku為20) 整個系統所需穩定時間拉長。 圖10 仿真波形(E的量化因子ke為14,EC的量化因子kec為18,U的的比例因子ku為15) 該圖在10s后添加了脈沖擾動信號。
結合翻閱資料可得,量化因子ke及kec 的大小對控制系統的動態性能影響很大,ke 選得較大時,系統的超調量也較大,過渡過程也較長。這一點也并不難理解,因為從理論上講,ke 增大,相當于縮短了誤差的基本論域,增大了誤差變量的控制作用,雖然能使上升時間變短,但由于超調過大,使得系統的過渡過程變長。kec 選擇越大系統超調越小,但系統的響應速度變慢,kec 對超調的遏制作用十分明顯。
其中,ke 對動態性能的影響是:ke 越大,調節死區越小,上升速率越大,調節時間越長,超調量越大,但是,ke 取得過大,將使系統產生較大的超調,調節時間增大,甚至產生震蕩,使系統不能穩定工作;而ke 過小,又使系統上升速率較小,系統調節隋性變大,同時也影響系統的穩態性能,使穩態精度降低。
kec對動態性能的影響是:kec大,反應較遲鈍,調節時間短,超調量大;kec 小,反應快,上升速率小,調節時間長,超調量小;而kec過小,將引起調節時間過長,嚴重時系統不能穩定工作。
對系統穩定性的影響在模糊控制系統中,一般不可能消除穩態誤差,更不可能消除誤差變化率。一般而言,ke 增加,穩態誤差將減小;kec 增大,穩態時誤差變化率也將減小。然而ke 、kec 對動態性能也有影響,因此必須兼顧兩方面的性能。
ku相當于常規系統中的比例增益,它主要影響控制系統的動態性能。一般ku增大,上升速率就快,超調量增大,響應時間減小,但是ku 過大,會導致系統輸出上升速率過大,從而產生過大的超調乃至振蕩和發散,嚴重時會影響穩態工作;而ku 過小,系統的前向增益很小,系統輸出上升速率較小,快速性變差,穩態精度變差,和一般控制系統不同的是,ku 一般不影響系統的穩態誤差。
同時應該指出,量化因子和比例因子的選擇并不是唯一的,可能有幾組不同的值,都能使系統獲得較好的響應特性。對于比較復雜的被控過程,有時采用一組固定的量化因和比例因子難以收到預期的控制效果,可以在控制過程中采用改變量化因子和比例因子的方法,來調整整個控制過程中不同階段上的控制特性,使其對復雜過程控制受到良好的控制效果。
以上的圖文Word格式文檔51黑下載地址:
 二級倒立擺模糊控制7級.doc
(2.61 MB, 下載次數: 21)
二級倒立擺模糊控制7級.doc
(2.61 MB, 下載次數: 21)
2021-5-16 16:55 上傳
點擊文件名下載附件
下載積分: 黑幣 -5
|