|
�������V���㷨��C�Z�Ԍ�(sh��)�F(xi��n) ժҪ����������ӑՓ�˿������V������ԭ���������㷨�Լ���(y��ng)���I(l��ng)���������U����kalman filter����Ϣ��Ӌ(j��)������(y��u)���ܡ����ؽ�B��(ji��n)��kalman filter algorithm�ľ��̣�ʹ��kalman filter�Ľ�(j��ng)��5��(g��)�w�F(xi��n)�(y��u)���f�w��ʽ�����̡�ͨ�^c�Z�Ծ�������?q��)��F(xi��n)kalman filter���(y��u)��Ӌ(j��)������
1 ���� Kalman Filter��һ��(g��)��Ч���f�w�V�����������Ԍ�(sh��)�F(xi��n)��һϵ�е����y(c��)���У���Ӌ(j��)��(d��ng)�B(t��i)ϵ�y(t��ng)�Ġ�B(t��i)����Դ��Rudolf Emil Kalman��1960��IJ�ʿՓ�ĺͰl(f��)����Փ�ġ�A New Approach to Linear Eiltering and Prediction Problems���������ԞV���c�A(y��)�y(c��)���}���·������������������ڰ����_����Ӌ(j��)��܉�E�A(y��)�y(c��)�ϑ�(y��ng)�óɹ����˺�kalman filterȡ���ش�l(f��)չ�����ơ����ďV����(y��ng)���ѽ�(j��ng)���^30�꣬�����C(j��)���ˌ�(d��o)�������ơ���������(sh��)��(j��)�ں�������܊�·�������_(d��)ϵ�y(t��ng)�Լ���(d��o)��ۙ�ȵȣ�����������V����(y��ng)����Ӌ(j��)��C(j��)�D��̎���������^Ę�R(sh��)�e���D��ָ�D��߅���z�y(c��)�ȵȡ� 2 kalman filter�(y��u)���f�w��Ӌ(j��) Kalman filter��һ��(g��)��optimal recursive data processing algorithm���(y��u)���f�w��(sh��)��(j��)̎��������������(du��)�ڽ�Q�ֵܴĆ��}�������(y��u)��Ч����������������õķ�������kalman filter�����ĵă�(n��i)�����w�F(xi��n)���(y��u)����Ӌ(j��)���f�w���c(di��n)��5�l��ʽ���eһ��(g��)���Ӂ�Ԕ��(x��)�f��5�l��ʽ���������x�� ���O(sh��)�҂�Ҫ�о��Č�(du��)����ijһ��(g��)���g�Ĝض���̖(h��o)����(du��)���Ҝ��f��һ��犃�(n��i)��һС�Εr(sh��)�g��(n��i)��ֵ�ǻ����ϲ�׃�Ļ���׃��������С��Ҳ�����f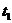 �r(sh��)�̵Ĝض� �r(sh��)�̵Ĝض� �� �� �r(sh��)�̵Ĝض� �r(sh��)�̵Ĝض�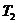 ������׃���� ������׃����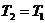 �����@��(g��)�^���У���?y��n)鮅���ض�߀��������׃�ģ��O(sh��)�Ўȵ�ƫ��҂����@�ȵ�ƫ����Ǹ�˹���� �����@��(g��)�^���У���?y��n)鮅���ض�߀��������׃�ģ��O(sh��)�Ўȵ�ƫ��҂����@�ȵ�ƫ����Ǹ�˹����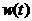 ��Ҳ�����f ��Ҳ�����f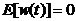 �� ��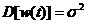 ������֮���҂�?c��)���һ��(g��)�ض�Ӌ(j��)�팍(sh��)�r(sh��)�y(c��)�����g�Ĝض�ֵ ������֮���҂�?c��)���һ��(g��)�ض�Ӌ(j��)�팍(sh��)�r(sh��)�y(c��)�����g�Ĝض�ֵ �����������߱������`����y(c��)�õĜض�ֵҲ�Dz���(zh��n)�_�ģ�Ҳ��(hu��)�͌�(sh��)�Hֵƫ��ȣ����@�ȵ�ƫ����ǜy(c��)���� �����������߱������`����y(c��)�õĜض�ֵҲ�Dz���(zh��n)�_�ģ�Ҳ��(hu��)�͌�(sh��)�Hֵƫ��ȣ����@�ȵ�ƫ����ǜy(c��)����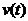 �����M�� �����M��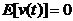 �� ��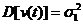 �� �� �˕r(sh��)�҂���(du��)���@��(g��)���g�ĜضȾ͵õ��˃ɂ�(g��)��(sh��)��(j��)��һ��(g��)�������(j��)��(j��ng)�(y��n)�õ��Ľ�(j��ng)�(y��n)ֵ ��һ��(g��)�ǏĜض�Ӌ(j��)�ϵõ��Ĝy(c��)��ֵ ��һ��(g��)�ǏĜض�Ӌ(j��)�ϵõ��Ĝy(c��)��ֵ ���Լ���������ĸ�˹����������;��w�v��kalman filter����Ӌ(j��)���g�ضȵ�ԭ���c���E�� ���Լ���������ĸ�˹����������;��w�v��kalman filter����Ӌ(j��)���g�ضȵ�ԭ���c���E�� Ҫ��Ӌ(j��)K�r(sh��)�̵Č�(sh��)�H�ض�ֵ������Ҫ����(j��)K-1�r(sh��)�̵Ĝض�ֵ�A(y��)�y(c��)K�r(sh��)�̵Ĝضȣ�����֮ǰ�҂�ӑՓ�� ����k-1�r(sh��)�̵Ĝض�ֵ�� ����k-1�r(sh��)�̵Ĝض�ֵ�� ����ô�A(y��)�y(c��)�˕r(sh��)�� ����ô�A(y��)�y(c��)�˕r(sh��)��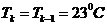 ������ԓֵ������ ������ԓֵ������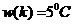 ��5�����@�ӵõ��ģ�����k-1�r(sh��)�̹�������(y��u)�ض�ֵ������ ��5�����@�ӵõ��ģ�����k-1�r(sh��)�̹�������(y��u)�ض�ֵ������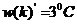 ���A(y��)�y(c��)������ ���A(y��)�y(c��)������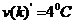 �����Կ��w������ �����Կ��w������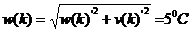 ���˕r(sh��)�ُĜض�Ӌ(j��)�ϵõ�K�r(sh��)�̵Ĝض�ֵ�� ���˕r(sh��)�ُĜض�Ӌ(j��)�ϵõ�K�r(sh��)�̵Ĝض�ֵ�� ���O(sh��)ԓ�y(c��)��ֵ������ ���O(sh��)ԓ�y(c��)��ֵ������ �� �� �F(xi��n)�ڰl(f��)�F(xi��n)���}�ˣ���k�r(sh��)���҂������˃ɂ�(g��)�ض�ֵ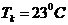 �� �� ��Ҫ���ǂ�(g��)�أ���(ji��n)�ε���ƽ���ѽ�(j��ng)���ܝM�㾫�ȵ�Ҫ���ˡ��҂������������ąf(xi��)����covariance���Дࡣ�f(xi��)����������w�F(xi��n)�ɂ�(g��)��̖(h��o)�����P(gu��n)�ԣ�ͨ�^�������Дൽ����ֵ���ƽ����A(y��)�y(c��)ֵ߀�ǜy(c��)��ֵ������kalman gain�� ��Ҫ���ǂ�(g��)�أ���(ji��n)�ε���ƽ���ѽ�(j��ng)���ܝM�㾫�ȵ�Ҫ���ˡ��҂������������ąf(xi��)����covariance���Дࡣ�f(xi��)����������w�F(xi��n)�ɂ�(g��)��̖(h��o)�����P(gu��n)�ԣ�ͨ�^�������Дൽ����ֵ���ƽ����A(y��)�y(c��)ֵ߀�ǜy(c��)��ֵ������kalman gain�� �����й�ʽӋ(j��)�� �����й�ʽӋ(j��)�� �� �� 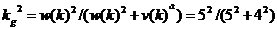 ������1�� ������1������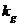 =0.78���҂����Թ����K�r(sh��)�̵Č�(sh��)�H�ض�ֵ�ǣ� =0.78���҂����Թ����K�r(sh��)�̵Č�(sh��)�H�ض�ֵ�ǣ� 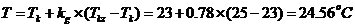 ������2�� ������2�����Կ����@��(g��)ֵ�ӽ��ڜض�Ӌ(j��)�y(c��)������ֵ�����Թ�������(y��u)�ض�ֵƫ��ض�Ӌ(j��)��ֵ�� �@�r(sh��)�҂��ѽ�(j��ng)�õ���K�r(sh��)�̵��(y��u)�ض�ֵ��������Ӌ(j��)K+1�r(sh��)�̵��(y��u)�ض�ֵ����Ȼkalman filter��һ��(g��)�(y��u)�����f�w̎����������ô�f�w���w�F(xi��n)��ԓ�㷨��һ��(g��)���ą���(sh��)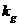 �ϣ��ɹ�ʽ��1�� �ϣ��ɹ�ʽ��1�� ���㷨��֪ÿ��Ӌ(j��)��r(sh��)�� ���㷨��֪ÿ��Ӌ(j��)��r(sh��)��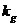 �Dz�һ�ӵġ��@���҂�Ҫ��Ӌ(j��)K+1�r(sh��)�̵��(y��u)�ض�ֵ���͵������K�r(sh��)�̵� �Dz�һ�ӵġ��@���҂�Ҫ��Ӌ(j��)K+1�r(sh��)�̵��(y��u)�ض�ֵ���͵������K�r(sh��)�̵� ��Ȼ��������ù�ʽ��2����Ӌ(j��)K+1�r(sh��)�̵��(y��u)�ض�ֵ���ɴ˿��Կ����҂�ֻ��֪����ʼ�r(sh��)�̵�ֵ��������(du��)��(y��ng)�ąf(xi��)�����Լ��y(c��)��ֵ���Ϳ����M(j��n)��kalman��Ӌ(j��)�ˡ� ��Ȼ��������ù�ʽ��2����Ӌ(j��)K+1�r(sh��)�̵��(y��u)�ض�ֵ���ɴ˿��Կ����҂�ֻ��֪����ʼ�r(sh��)�̵�ֵ��������(du��)��(y��ng)�ąf(xi��)�����Լ��y(c��)��ֵ���Ϳ����M(j��n)��kalman��Ӌ(j��)�ˡ� 3Kalman Filter Algorithm ������һ��(g��)�xɢ�����^�̞���ӑՓkalman filter algorithm��ԓϵ�y(t��ng)����һ��(g��)�����ַ��́������� 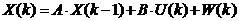 ������3�� ������3��
 ������4�� ������4��
��3��ʽ�ͣ�4��ʽ�У� ��K�r(sh��)�̵�ϵ�y(t��ng)��B(t��i)�� ��K�r(sh��)�̵�ϵ�y(t��ng)��B(t��i)�� ��K�r(sh��)�̌�(du��)ϵ�y(t��ng)�Ŀ�������A��B��ϵ�y(t��ng)����(sh��)����(du��)�ڶ�ģ��ϵ�y(t��ng)������?y��u)��ꇡ?img id="aimg_R3n4w" onclick="zoom(this, this.src, 0, 0, 0)" class="zoom" width="36" height="21" src="http://c.51hei.com/a/huq/a/a/c/23/23.038.jpg" border="0" alt="" />��K�r(sh��)�̵Ĝy(c��)��ֵ��H�ǜy(c��)��ϵ�y(t��ng)�ą���(sh��)����(du��)�ڶ��y(c��)��ϵ�y(t��ng)��H���ꇡ� ��K�r(sh��)�̌�(du��)ϵ�y(t��ng)�Ŀ�������A��B��ϵ�y(t��ng)����(sh��)����(du��)�ڶ�ģ��ϵ�y(t��ng)������?y��u)��ꇡ?img id="aimg_R3n4w" onclick="zoom(this, this.src, 0, 0, 0)" class="zoom" width="36" height="21" src="http://c.51hei.com/a/huq/a/a/c/23/23.038.jpg" border="0" alt="" />��K�r(sh��)�̵Ĝy(c��)��ֵ��H�ǜy(c��)��ϵ�y(t��ng)�ą���(sh��)����(du��)�ڶ��y(c��)��ϵ�y(t��ng)��H���ꇡ�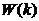 �� ��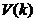 �քe��ʾϵ�y(t��ng)�͜y(c��)���^���е�����ʹ��kalman filter��Ӌ(j��)�r(sh��)���҂��J(r��n)�����M���˹����ģ�ͣ��O(sh��) �քe��ʾϵ�y(t��ng)�͜y(c��)���^���е�����ʹ��kalman filter��Ӌ(j��)�r(sh��)���҂��J(r��n)�����M���˹����ģ�ͣ��O(sh��)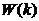 �� ��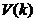 ��covariance�քe��Q��R�� ��covariance�քe��Q��R�� ӑՓkalman filter algorithm��5��(g��)��(j��ng)����Ĺ�ʽ�� ��һ�����A(y��)�y(c��)�F(xi��n)�ڵĠ�B(t��i)��  ������5�� ������5��
ʽ��5����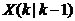 ��������һ��B(t��i)�A(y��)�y(c��)�ĽY(ji��)���� ��������һ��B(t��i)�A(y��)�y(c��)�ĽY(ji��)���� ����һ�r(sh��)�̵��(y��u)�A(y��)�y(c��)ֵ�� ����һ�r(sh��)�̵��(y��u)�A(y��)�y(c��)ֵ��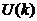 ��F(xi��n)�ڠ�B(t��i)�Ŀ�����������]�У����Ԟ�0�� ��F(xi��n)�ڠ�B(t��i)�Ŀ�����������]�У����Ԟ�0�� ��(j��ng)�^��ʽ��5����ϵ�y(t��ng)�Y(ji��)���ѽ�(j��ng)�����ˣ���(du��)��(y��ng)�� 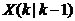 ��covariance߀�]�и��£���P��ʾcovariance�� ��covariance߀�]�и��£���P��ʾcovariance�� 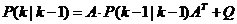 ������6�� ������6��
ʽ��6����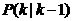 �� �� ��(du��)��(y��ng)��covariance�� ��(du��)��(y��ng)��covariance��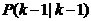 �� ��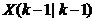 ��(du��)��(y��ng)��covariance�� ��(du��)��(y��ng)��covariance�� �� ��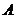 ���D(zhu��n)�þ�ꇡ�Q��ϵ�y(t��ng)��������5���ͣ�6��ʽ����kalman filter�е�ǰ�ɂ�(g��)��ʽ����(du��)ϵ�y(t��ng)���A(y��)�y(c��)������ϵ�y(t��ng)���A(y��)�y(c��)��������Ҫ�����y(c��)��ֵ�M(j��n)�й�Ӌ(j��)�ˡ� ���D(zhu��n)�þ�ꇡ�Q��ϵ�y(t��ng)��������5���ͣ�6��ʽ����kalman filter�е�ǰ�ɂ�(g��)��ʽ����(du��)ϵ�y(t��ng)���A(y��)�y(c��)������ϵ�y(t��ng)���A(y��)�y(c��)��������Ҫ�����y(c��)��ֵ�M(j��n)�й�Ӌ(j��)�ˡ� 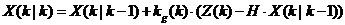 ������7�� ������7��
�����������֪���ˌ�(sh��)�F(xi��n)�f�w��ÿ�ε� ���nj�(sh��)�r(sh��)���µġ� ���nj�(sh��)�r(sh��)���µġ� 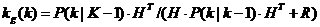 ������8�� ������8��
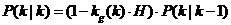 ������9�� ������9��
�@��ÿ�� �� ��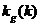 ����Ҫǰһ�r(sh��)�̵�ֵ�����£��f�w�Ĺ�Ӌ(j��)��ȥ����5��~��9��ʽ����kalman filter algorithm����l���Ĺ�ʽ�� ����Ҫǰһ�r(sh��)�̵�ֵ�����£��f�w�Ĺ�Ӌ(j��)��ȥ����5��~��9��ʽ����kalman filter algorithm����l���Ĺ�ʽ�� 4 ����C�Z�Ծ��̌�(sh��)�F(xi��n)Kalman Filter Algorithm Ҫ���ǽo��һ��(g��)�̶�����Ȼ���ɜy(c��)��ֵ��ʹ��kalman filter��Ӌ(j��)ϵ�y(t��ng)�挍(sh��)ֵ�� ���˾��̺�(ji��n)�Σ��Ҍ���5��ʽ�е�A=1�� =0����5��ʽ�Č����������ʽ�� =0����5��ʽ�Č����������ʽ��  ������10�� ������10��
ʽ��6���Č��飬 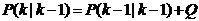 ������11�� ������11��
����H=1��ʽ��7������8������9���ɸČ��飬  ������12�� ������12��
 ������13�� ������13��
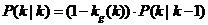 ������14�� ������14��
ʹ��C�Z�Ծ��̌�(sh��)�F(xi��n)�������㷨���� x_mid=x_last; //x_last=x(k-1|k-1),x_mid=x(k|k-1) p_mid=p_last+Q; //p_mid=p(k|k-1),p_last=p(k-1|k-1),Q=�� kg=p_mid/(p_mid+R); //kg��kalman filter��R���� z_measure=z_real+frand()*0.03;//�y(c��)��ֵ x_now=x_mid+kg*(z_measure-x_mid);//��Ӌ(j��)�����(y��u)ֵ p_now=(1-kg)*p_mid;//�(y��u)ֵ��(du��)��(y��ng)��covariance p_last = p_now; //����covarianceֵ x_last = x_now; //����ϵ�y(t��ng)��B(t��i)ֵ 5 �㷨�y(c��)ԇ ���˜y(c��)ԇkalman filter algorithm�����O(sh��)Ӌ(j��)��һ��(g��)��(ji��n)�Ό�(sh��)�(y��n)�����(y��n)�Ckalman filter�ă�(y��u)���ԡ������нo��һ��(g��)��ֵ��Ȼ��o��һ�M�y(c��)��ֵ���(y��n)�Ckalman filter��ֵ�Ĝ�(zh��n)�_�ԡ� ����(j��)kalman filter algorithm���҂���Ҫ�o��ϵ�y(t��ng)��ʼֵx_last��ϵ�y(t��ng)��Q�͜y(c��)����R���Լ���ʼֵ����(du��)��(y��ng)�ąf(xi��)����P_last�������(y��n)�C��(y��u)���ԣ�߀��Ҫ�o���挍(sh��)ֵz(m��)_real��Ӌ(j��)��kalman filter�`��error_kalman�Լ��y(c��)���`��error_measure�Լ�����?c��)����ε��?j��)���е��۷e�`��۷ekalman�`��sumerror_kalman���۷e�y(c��)���`��sumerror_measure�� ��(sh��)�(y��n)�нo��x_last=0��p_last=0,Q=0.018,R=0.0542.��(sh��)�(y��n)�п���ͨ�^�m��(d��ng)��׃Q��R���@�ø��õĹ�Ӌ(j��)�Y(ji��)����Ҳ���Ը�׃p_last��x_last��ֵ������kalman filter�nj�(du��)�f(xi��)������f�w�㷨����Ӌ(j��)��̖(h��o)��(sh��)��(j��)�ģ�����p_last��(du��)�㷨�Y(ji��)����Ӱ푺ܴD3���f�����@һ��r�������ڳ�ʼ�r(sh��)���Ѕf(xi��)����������\(y��n)���^�����㷨�۷e�`����ȳ�ʼ�r(sh��)�]���`��ľͱ��^�� �o��ֵ��z_real=0.56�r(sh��)�\(y��n)�нY(ji��)����D1��ʾ�� �D1 ��ֵ��0.56���\(y��n)�нY(ji��)�� �o��ֵz(m��)_real=3.32�r(sh��)���\(y��n)�нY(ji��)����D2 �D2 ��ֵ��3.32���\(y��n)�нY(ji��)�� �D3��Q��R��׃��p_last=0.02��x_last=0��z_real=0.56�r(sh��)�Ĝy(c��)ԇ�Y(ji��)����ͨ�^��ǰ�ɴνY(ji��)�����^�l(f��)�F(xi��n)p_last��(du��)��Ӌ(j��)�Y(ji��)��Ӱ��^������֪�@�N�F(xi��n)���Ƿ���kalman filter�ģ�ͨ�^��׃Q��R��ֵҲ�ܸ����㷨�����ܣ����nj�(sh��)�H�������҂������ܿ����@�ɂ�(g��)���� �D3 ��׃p_last�Ĝy(c��)ԇ�Y(ji��)�� 6 �Y(ji��)Փ ����ͨ�^��(du��)kalman filter algorithm������̽ӑ����(du��)kalman filter���˸���̵��J(r��n)�R(sh��)�������˺��ĵ�5�l��ʽ���������x���Լ�kalman filter��˼�룬��ͨ�^�����㷨���̌�(sh��)�`���(y��n)�C��kalman filter�ڔ�(sh��)��(j��)̎������ă�(y��u)�����ܡ� ����ͨ�^��(sh��)�(y��n)�Y(ji��)��������kalman filter algorithm�ı��|(zh��)��(du��)ÿ�ι�Ӌ(j��)�a(ch��n)���ąf(xi��)�����f�w�Y(ji��)�Ϯ�(d��ng)ǰ�y(c��)��ֵ����Ӌ(j��)ϵ�y(t��ng)��(d��ng)ǰ����Ѡ�B(t��i)����Ҫ�����㷨�����ܾͱ��Ҫ�M���ܵĜpСϵ�y(t��ng)���͜y(c��)��������(y��u)�����pС��Ӌ(j��)�ąf(xi��)��� �����īI(xi��n) [1]�T�Ə�(qi��ng).C�����O(sh��)Ӌ(j��)(������)[M].����:���A��W(xu��)������,2005,91~130. [2]��ƽ�h(yu��n),�S����.����(li��n)�Ͽ������V���Ķ���������Ϣ�ں��㷨���䑪(y��ng)��[J].늙C(j��)�c���ƌW(xu��)��(b��o),2001,9(5): 204-207. [3]�h����,�n����,�Α�(zh��n)��.���ڶ�����V���������m��(y��ng)�������ں�[J].ϵ�y(t��ng)�����c��Ӽ��g(sh��),2004,5(26):311-313. [4]��ؕ��(ji��n),������. һ�N��(w��n)����ֱ����ȡ�㷨[J].ܛ���W(xu��)��(b��o),2001,11(11):1660-1665.
�����Դ����
#include "stdio.h" #include "stdlib.h" #include "math.h" double frand() { return 2*((rand()/(double)RAND_MAX) - 0.5); //�S�C(j��)��} void main() { float x_last=0; float p_last=0.02; float Q=0.018; float R=0.542; float kg; float x_mid; float x_now; float p_mid; float p_now; float z_real=0.56;//0.56 float z_measure; float sumerror_kalman=0; float sumerror_measure=0; int i; x_last=z_real+frand()*0.03; x_mid=x_last; for(i=0;i<20;i++) { x_mid=x_last; //x_last=x(k-1|k-1),x_mid=x(k|k-1) p_mid=p_last+Q; //p_mid=p(k|k-1),p_last=p(k-1|k-1),Q=�� kg=p_mid/(p_mid+R); //kg��kalman filter��R���� z_measure=z_real+frand()*0.03;//�y(c��)��ֵ x_now=x_mid+kg*(z_measure-x_mid);//��Ӌ(j��)�����(y��u)ֵ p_now=(1-kg)*p_mid;//�(y��u)ֵ��(du��)��(y��ng)��covariance printf("Real position: %6.3f \n",z_real); //�@ʾ��ֵ printf("Mesaured position: %6.3f [diff:%.3f]\n",z_measure,fabs(z_real-z_measure)); //�@ʾ�y(c��)��ֵ�Լ���ֵ�c�y(c��)��ֵ֮�g���`�� printf("Kalman position: %6.3f [diff:%.3f]\n",x_now,fabs(z_real - x_now)); //�@ʾkalman��Ӌ(j��)ֵ�Լ���ֵ�Ϳ�������Ӌ(j��)ֵ���`�� sumerror_kalman += fabs(z_real - x_now); //kalman��Ӌ(j��)ֵ���۷e�`�� sumerror_measure += fabs(z_real-z_measure); //��ֵ�c�y(c��)��ֵ���۷e�`�� p_last = p_now; //����covarianceֵ x_last = x_now; //����ϵ�y(t��ng)��B(t��i)ֵ } printf("���w�y(c��)���`�� : %f\n",sumerror_measure); //ݔ���y(c��)���۷e�`�� printf("���w�������V���`��: %f\n",sumerror_kalman); //ݔ��kalman�۷e�`�� printf("�������`����ռ����: %d%% \n",100-(int)((sumerror_kalman/sumerror_measure)*100)); }
���ψD�ĵ�Word��ʽ�ęn���d(��(n��i)�ݺͱ��W(w��ng)��ϵ�һģһ��,���㱣��):
 �������V���㷨C�Z�Ԍ�(sh��)�F(xi��n).zip
(99.89 KB, ���d��(sh��): 445)
�������V���㷨C�Z�Ԍ�(sh��)�F(xi��n).zip
(99.89 KB, ���d��(sh��): 445)
2018-12-14 11:09 �ς�
�c(di��n)���ļ������d����
���d�e��: �ڎ� -5
| 
 ����TQQ:125739409;���g(sh��)����QQȺ281945664
����TQQ:125739409;���g(sh��)����QQȺ281945664