直接查表就好了

其實既然使用了能計算對數的單片機，那么是不是直接查表就好了，畢竟廠家提供的數據表也只是整數溫度，那么計算出來的小數溫度又是否能代表精度呢

這個問題的討論對于我理解NTC的計算很有幫助。 謝謝你！

hui7279 發表于 2024-1-20 16:17
REF=94980*2069*(advalue_NT0-advalue_NT100);
//將ADC值轉換為校準的ADC值
REF=REF/(94980*(advalue_N ...

//據Steinhart-hart方程計算溫度值，RT可能用Tr表達會更準確：
//據Steinhart-hart方程計算溫度值，是最后Rt值已轉化為溫度值Tr，用同一個變量減少內存消耗

REF=94980*2069*(advalue_NT0-advalue_NT100);
//將ADC值轉換為校準的ADC值
REF=REF/(94980*(advalue_NT100-advalue_NTShort)-2069*(advalue_NT0-advalue_NTShort));
//將ADC值轉換為硬件的實際電壓值
VREF=(advalue_NT100-advalue_NTShort)*((2069+REF)/2069);
//將ADC值電壓轉換基準點，與硬件接高低位有關
advalue=advalue-advalue_NTShort;
//將電壓值轉換為電阻值
  Rt=(advalue*REF)/(VREF-advalue);
//據Steinhart-hart方程計算中間值ln(Rt)
  LNR=log(Rt);
//據Steinhart-hart方程計算溫度值，RT最后轉化為Tr，用同一個變量節約內存
  Rt=(1/(0.00093494+(0.0002211*LNR)+(0.0000001275*LNR*LNR*LNR)))-273.15;
/******************************************
Steinhart-Hart方程計算法：
1/T = A + B*ln(R) + C*[ln(R)]^3
由于：T值在公式中是用熱力學溫度單位K，攝氏度就要減273.15；
此公式中：A＝0.0009349， B＝0.0002211， C ＝0.0000001275
ABC值與硬件NTC有關，不同廠家的NTC表值需要用不同參數；
---------------------------------------------------
ABC值的計算方法：
具體可以將要用到的三個關鍵溫度點值：T0、T1、T2、R0、R1、R2；
利用計算ln(R0)、ln(R1)、ln(R2)；代入Steinhart-Hart方程（溫度值要+273.15）
得到三元一次方程組，可以用矩陣法解方程法，具體查常用C算法函數；
也可用EXCEL的方法解三元一次方程組，具體可以百度
************************************************/

剛好也在研究一個儀器的NTC測溫電路，界面顯示是一個電壓值多少mv，旁邊一個溫度值。能查到系統的a b c值，正在研究中，有什么進展大家共同分享

Y_G_G 發表于 2022-6-9 13:31
想要精度高就查表

我認為這個方程好像貝塞爾曲線通過控制點擬合的結果

路明非. 發表于 2022-6-8 22:19
知道原理才能改進提高啊，這個利用三個點校準也是為了提高測溫的精度，而且這樣測溫精度高反應速度也快

想要精度高就查表

溫度計算，Steinhart-Hart方程和B值法

使用Steinhart-Hart方程或者B值計算方法將熱敏電阻的電阻值轉換為溫度讀數。

  Steinhart-Hart方程計算法：

1/T = A + B*ln(R) + C*[ln(R)]

這里: T 為絕對溫度K(開爾文溫度)，R 單位是歐姆

. 溫度系數B值計算法：

Rt = R(25℃)*exp[B*(1/T - 1/298.15)]

這里：T 為絕對溫度K(開爾文溫度 = 273.15)，R(25℃) 是熱敏電阻在 25℃時的阻值 (單位為Ω)，exp是e的n次方；

3. C語言實現的溫度計算公式

Tsteinhart = 1/(A+B*log(Rth)+C*pow(log(Rth),3))-273.15;

Tbeta = 1/(1/(273.15+25)+1/Beta*log(Rth/R25))-273.15;


  ln、log、lg在數學公式中和c語言中的區別：

參考：cplusplus的"<cmath> (math.h) - C++ Reference"這篇文章

數學中log是對數符號，右邊寫真數和底數（上面是真數,下面是底數）lg是以10為底數（例lg100=2）（lg為常用對數）ln是以e為底數（lne2=2）（ln為自然對數 e=2.718281828459045...）

  c語言里面只有兩個函數log和log10，其中函數 log(x) 表示是以e為底的自然對數，即 ln(x)函數。 log10(x) 以10為底的對數，即 lg(x)。以其它數為底的對數用換底公式來表示：loga(b)=ln(b)/ln(a)，C語言表示成log(b)/log(a)。

Hephaestus 發表于 2022-6-8 21:10
你看了代碼再來發言好不好？什么都不懂就上來胡說很沒有禮貌的。樓主明顯是個30k的NTC，B值未知。而且標 ...

樓主所列代碼確實沒看懂。只知道NTC是在25度條件下的標稱精度，25~50度的標稱B值。偏離標準溫度越多，精度和B值誤差越大。用固定公式計算，除非對NTC元件預選，否則很難批量生產。大佬如有自動糾偏的方法，還望分享。 中國NTC溫度傳感器150K B3950 ±1%.rar (28.31 KB, 下載次數: 19)

2022-6-9 07:29 上傳

點擊文件名下載附件

Y_G_G 發表于 2022-6-8 21:46
如果不是內存實在不夠用,NTC用查表是常用也是最實在的
至于這個方程的原理,它是兩個老外一個叫Steinhart, ...

你錯了，Steinhart-hart方程用這兩句就解決完了，完全沒有任何難度，不存在看不懂的地方。
  LNR=log(Rt);
  Rt=(1/(0.00093494+(0.0002211*LNR)+(0.0000001275*LNR*LNR*LNR)))-273.15;

樓主的問題是第一句的Rt是怎么來的，這個前面的代碼也太復雜了，要動手算算。

Y_G_G 發表于 2022-6-8 21:46
如果不是內存實在不夠用,NTC用查表是常用也是最實在的
至于這個方程的原理,它是兩個老外一個叫Steinhart, ...

知道原理才能改進提高啊，這個利用三個點校準也是為了提高測溫的精度，而且這樣測溫精度高反應速度也快

如果不是內存實在不夠用,NTC用查表是常用也是最實在的
至于這個方程的原理,它是兩個老外一個叫Steinhart,一個叫Hart,合起來就是Steinhart-Hart,根據熱敏電阻的特性研究出來的
個人感覺原理什么的并不重要,你上網也不一定能查得到,會用就行
電子編程這一塊,那么多恐怖的公式,哪能個個都知道原理呀

wulin 發表于 2022-6-8 20:40
樓主所述NTC熱敏電阻可能是PT100、PT1000等鉑電阻。普通NTC熱敏電阻幾乎不可能通過公式計算獲得較準確溫度 ...

你看了代碼再來發言好不好？什么都不懂就上來胡說很沒有禮貌的。樓主明顯是個30k的NTC，B值未知。而且標定了三個點，1）短路NTC測試放大以及ADC環節的誤差；2）0度時NTC的值；3）100度時NTC的值。

wulin 發表于 2022-6-8 20:40
樓主所述NTC熱敏電阻可能是PT100、PT1000等鉑電阻。普通NTC熱敏電阻幾乎不可能通過公式計算獲得較準確溫度 ...

實際情況是ntc測溫的確用的公式計算的而且測溫精度還很高，具體參考Steinhart-hart方程

樓主所述NTC熱敏電阻可能是PT100、PT1000等鉑電阻。普通NTC熱敏電阻幾乎不可能通過公式計算獲得較準確溫度值。NTC熱敏電阻不同廠家產品溫阻曲線差異較大，同一廠家相同規格的產品電參數也有較大離散性。不適合用公式計算溫度值。除非對精度要求很低。

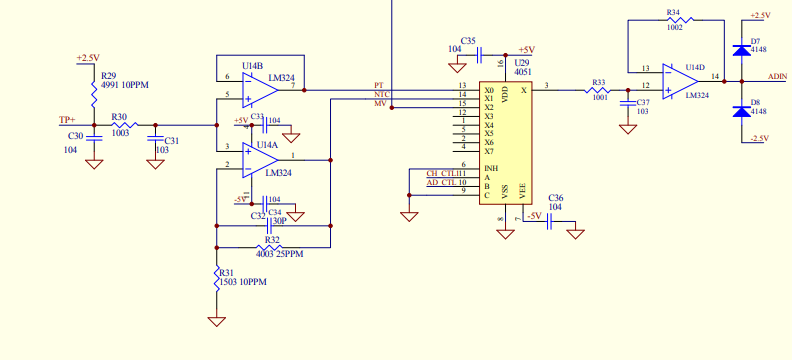
Hephaestus 發表于 2022-6-8 19:07
這電路圖畫的只能說一個字：服！連NTC在哪里都可以看不到。

tp+是ntc

Hephaestus 發表于 2022-6-8 19:07
這電路圖畫的只能說一個字：服！連NTC在哪里都可以看不到。

TP+是ntc

路明非. 發表于 2022-6-8 19:02
這是電路

這電路圖畫的只能說一個字：服！連NTC在哪里都可以看不到。

你的問題跟硬件相關，沒有電路圖我們也不會算命。

17337161031 發表于 2022-6-8 18:45
中間那一段代碼就是對采集到的數據的轉換，那就是計算的啊，你寫成公式的形式就比較清晰了

94980和2069是0度和100度對應的阻值

17337161031 發表于 2022-6-8 18:45
中間那一段代碼就是對采集到的數據的轉換，那就是計算的啊，你寫成公式的形式就比較清晰了

電阻值具體是怎么從3個ad量算出來的呢？

中間那一段代碼就是對采集到的數據的轉換，那就是計算的啊，你寫成公式的形式就比較清晰了

/*************************************************
函數名稱：  NTC30K_function
函數功能：  NTC30K計算函數
函數形參：  
            advalue：adc值
            advalue_NT0：校正的0度ADC
            advalue_NT100：校正的100度ADC
            advalue_NTShort：校正的偏移ADC
函數返回值：溫度值
*************************************************/
FP32 NTC30K_function(FP32 advalue,FP32 advalue_NT0,FP32 advalue_NT100,FP32 advalue_NTShort)
{
  FP32 REF,VREF,Rt,LNR;
  REF=94980*2069*(advalue_NT0-advalue_NT100);
  REF=REF/(94980*(advalue_NT100-advalue_NTShort)-2069*(advalue_NT0-advalue_NTShort));
  VREF=(advalue_NT100-advalue_NTShort)*((2069+REF)/2069);
  advalue=advalue-advalue_NTShort;
  Rt=(advalue*REF)/(VREF-advalue);
  LNR=log(Rt);
  Rt=(1/(0.00093494+(0.0002211*LNR)+(0.0000001275*LNR*LNR*LNR)))-273.15;
  return(Rt);
}