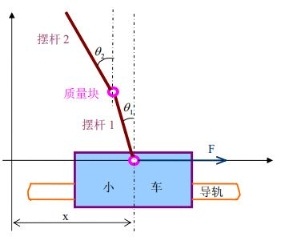
倒立擺是進行控制理論研究的典型實驗平臺,許多抽象的控制理論概念,如系統的穩定性、可觀性及可控性等都可以通過該系統直觀地表示出來。因此,近幾年來,該系統已經成為控制領域的研究熱點。
倒立擺系統是一個典型的非線性、強耦合、多變量和不穩定系統。在控制研究領域有著代表性的意義。倒立擺作為控制系統的被控對象,許多抽象的控制概念都可以通過它直觀的表現出來。本次課設我選用以二級倒立擺為研究對象,采用牛頓力學定律進行數學建模,利用二次型最優控制器( LQR)求出最優狀態反饋矩陣K,經過對Q和R兩個加權矩陣的選取實現二級倒立擺的自動控制。該方法為多變量反饋系統的設計提供了有效的分析法,可適于時變系統,處理擾動信號和測量噪聲,處理有限和無限的時間區間。
1 系統建模
1.1相關數據

圖 1 直線兩級倒立擺物理模型
首先,對該系統做如下假設:
1)小車、一級擺桿和二級擺桿都是剛體。
2)皮帶輪與同步帶之間無相對滑動,且同步帶不會拉伸變長。
3)小車與導軌之間的摩擦力與小車速度成正比。
4)各級擺桿與轉軸間的轉動摩擦力矩與擺桿的角速度成正比。
表1 二級倒立擺各物理參數:
符號 | 含義 | 實際系統參數 |
M | 小車質量 | 1.32kg |
m1 | 下擺桿質量 | 0.04kg |
m2 | 上擺桿質量 | 0.132kg |
m3 | 質量塊質量 | 0.208kg |
θ1 | 下擺擺桿與垂直向上方向的夾角 | θ1 |
θ2 | 上擺擺桿與垂直向上方向的夾角 | θ2 |
l1 | 下擺擺桿轉動中心到擺桿質心的距離 | 0.09m |
l2 | 上擺擺桿轉動中心到擺桿質心的距離 | 0.27m |
F | 作用在小車上的外力 |
|
1.2理論依據
1.2.1 受力分析
其中 L 為拉格朗日算子,q 為系統的廣義坐標,T 為系統的動能,V 為系統的
勢能。
其中 i=1,2,3……n, i f 為系統在第 i 個廣義坐標上的外力,在二級倒立擺系統中,系統的廣義坐標有三個廣義坐標,分別為 x, θ1, θ2 。
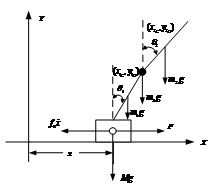
圖2 直線二級倒立擺受力分析
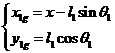
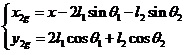
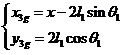
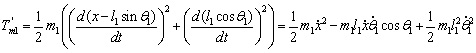
同理帶入(1-7),求出擺桿2的動能為:
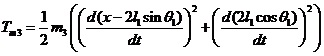
因此將(1-7)(1-8)(1-9)帶入(1-3),可以得到系統動能為
從而得到Lagrange函數為
1.2.2 列出Lagrange方程
由于在廣義坐標![]() 上均無外力作用,故列寫Lagrange方程得到
上均無外力作用,故列寫Lagrange方程得到
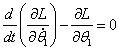 (2-1)
(2-1)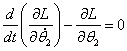 (2-2)
(2-2)將L代入式(2-1)和(2-2)得到
1.3 倒立擺運動方程的線性化處理
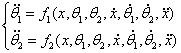
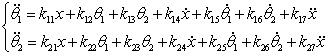
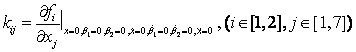
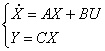
根據系統狀態變量直接的關系,寫出系統的狀態空間方程為:
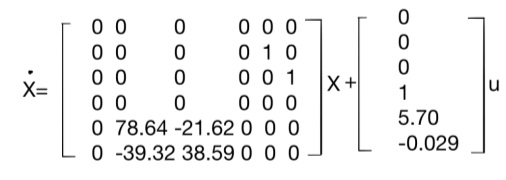
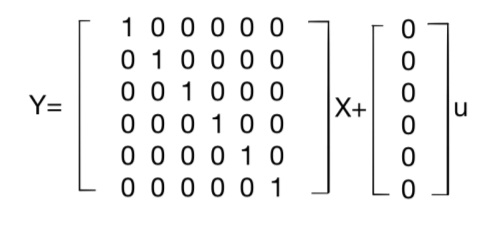
1.4 能控能觀性檢測
1.4.1能控性檢測
1.4.2觀測性檢測
2 模糊控制器的設計
2.1模糊控制器基本原理
模糊控制是以模糊集理論、模糊語言變量和模糊邏輯推理為基礎的一種智能控制方法,它是從行為上模仿人的模糊推理和決策過程的一種智能控制方法。該方法首先將操作人員或專家經驗編成模糊規則,然后將來自傳感器的實時信號模糊化,將模糊化后的信號作為模糊規則的輸入,完成模糊推理,將推理后得到的輸出量加到執行器上。
簡言之,模糊控制器會將輸入的誤差和誤差變化量的精確值進行模糊化,然后將模糊值進行邏輯推理,最后將得到的模糊值去模糊化再送出。
模糊控制器的結構如圖3所示。控制器由4個基本部分組成,即模糊化接口、知識庫、推理機、解模糊接口。
根據前面介紹的二級倒立擺穩定控制思想,采用融合技術設計一個線性融合函數,把多個變量融合成為綜合誤差E和綜合誤差變化率EC,這就可以使模糊控制器的設計大為簡化。如圖4。
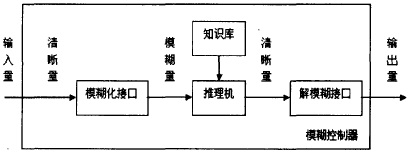
圖3模糊控制器的結構
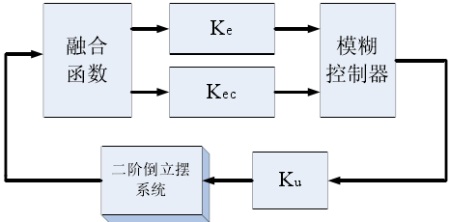
圖4 采用融合技術的模糊控制器
2.2模糊控制器設計步驟
(1)確定模糊控制器的輸入變量和輸出變量(即控制量);
(2)設計模糊控制器的控制規則;
(3)進行模糊化和解模糊化;
(4)選擇模糊控制器的輸入變量及輸出變量的論域,并確定模糊控制器的參數(如量化因子、比例因子);
(5)編制模糊控制算法的應用程序;
2.3模糊規則表

If EC=NB and E=NB then U=NB ;
If EC=NB and E=NM then U=NB
If EC=NB and E=NS then U=NB
If EC=NB and E=ZE then U=NM
If EC=NB and E=PS then U=NM
If EC=NB and E=PM then U=NS
If EC=NM and E=NB then U=NB ……
2.4利用融合函數設計
基于LQR理論來為二級倒立擺的狀態方程設計一個狀態反饋矩陣K和降維矩陣G,將六個狀態變量綜合成兩個變量,即綜合誤差E和綜合誤差變化率EC。并通過LQR仿真,得出輸入輸出數據對,根據得出的數據,計算并制定出模糊規則。
利用最優控制理論計算出一組可以讓二級倒立擺穩定的狀態反饋矩陣K:![]() (2-1)
(2-1)
最優控制性能指標函數為:
![]() (2-2)
(2-2)
通過使性能指標函數式(6-1)為最小,可求得:
![]() (2-3)
(2-3)
求解如下Ricatti方程可得到矩陣P。
![]() (2-4)
(2-4)
性能指標函數中,矩陣Q和矩陣R這兩個參數需要定義,是用來平衡系統對輸入量和狀態量的敏感程度的。它們對閉環系統的動態性能影響很大。在倒立擺系統中,Q,R分別用來對狀態向量X和輸入控制量u進行平衡加權的。一般情況下,R增加時,控制力減小,角度變化變小,跟隨速度變慢。而Q中某元素增加時,其對應的狀態變量的響應速度增加,其它狀態變量的響應速度相對減慢。為了使得反饋矩陣K更合理,對矩陣Q, R的選取一定要盡量恰當。通過反復的測試,在實際系統的控制過程中,選取

基于MATLAB強大的矩陣運算以及它豐富的內部函數,利用K=lqr(A,B,Q,R)命令通過計算,可得到狀態反饋矩陣K:
K=[17.3205,111.7009,-200.6791,18.6848, 2.6899,-32.5784]
本文應用歸一化思想設計降維矩陣G。從上面的結論中得知狀態矩陣K中包含六個元素,分別代表著六個狀態變量的權值。根據歸一化思想,每個元素均除以矩陣K的范數,為了把六個狀態變量合并成兩個變量,設計如式(2-5 )形式的矩陣,利用狀態反饋陣K構造出降維矩陣G:
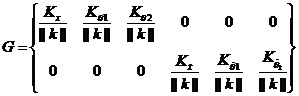 (2-5)
(2-5)
其中,![]()
把所得狀態反饋陣K的值代入式(6-5 )得到G:![]()
最后,通過降維矩陣G把六個狀態變量X綜合為兩個變量,稱為綜合誤差E和綜合誤差變化率EC。
![]() (2-6)
(2-6)
2.5模糊控制器的輸入輸出論域及模糊集合的劃分
首先對系統進行采樣,粗略確定輸入輸出論域:位置[-0.2,0.2],速度[-1,1],下擺角[-0.15,0.15],下擺角速度[-4 , 4]上擺角[-0.08, 0.08],上擺角速度[-0.8, 0.8],控制力[-45,45]。為簡化,綜合誤差E、綜合誤差變化域EC和輸出量化域均為[-3,3]。
可大致估算E的量化因子為14,EC的量化因子為18,U的的比例因子為15。
3 matlab仿真
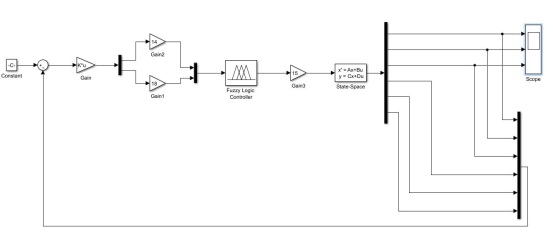
圖5 模型建立
該模型Constant初值我設定為0,融合矩陣![]() ,系統矩陣A=
,系統矩陣A= ,輸入矩陣B=
,輸入矩陣B=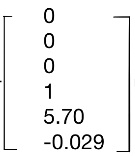 ,
,
輸出矩陣C= ,直聯矩陣D=
,直聯矩陣D= 。初始,我選定E的量化因子為14,EC的量化因子為18,U的的比例因子為15。
。初始,我選定E的量化因子為14,EC的量化因子為18,U的的比例因子為15。
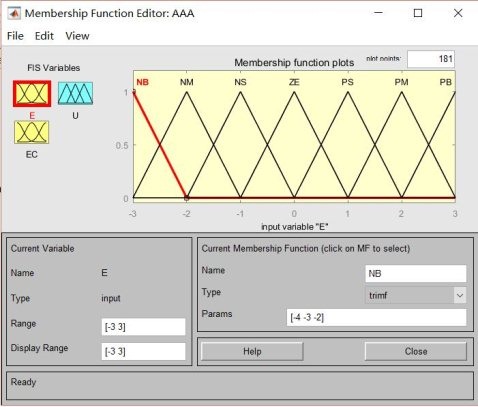
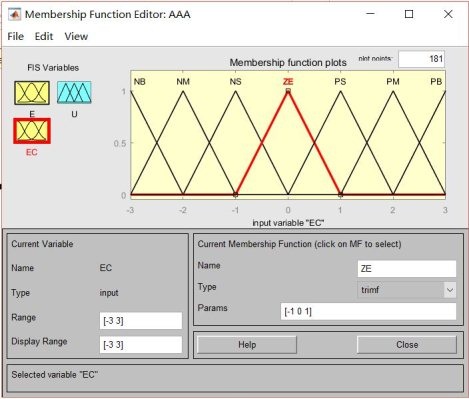
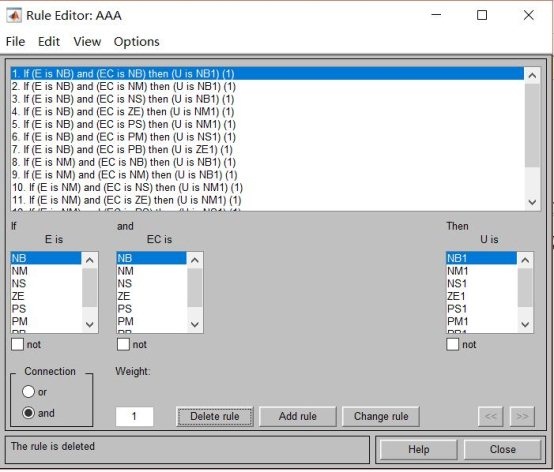
表3 模糊規則表
EC E | NB | NM | NS | ZE | PS | PM | PB |
NB | NB | NB | NB | NM | NM | NS | ZE |
NM | NB | NB | NM | NM | NS | ZE | PS |
NS | NB | NM | NM | NS | ZE | PS | PM |
ZE | NM | NS | NS | ZE | PS | PM | PM |
PS | NM | ZE | ZE | PS | PM | PM | PB |
PM | NS | PS | PS | PM | PM | PB | PB |
PB | ZE | PM | PM | PM | PB | PB | PB |
If EC=NB and E=NB then U=NB ;
If EC=NB and E=NM then U=NB
If EC=NB and E=NS then U=NB
If EC=NB and E=ZE then U=NM
If EC=NB and E=PS then U=NM
If EC=NB and E=PM then U=NS
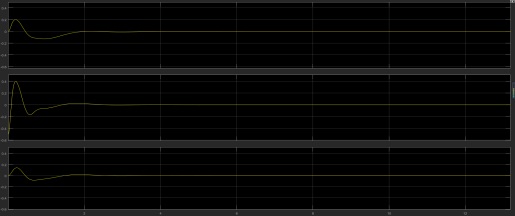

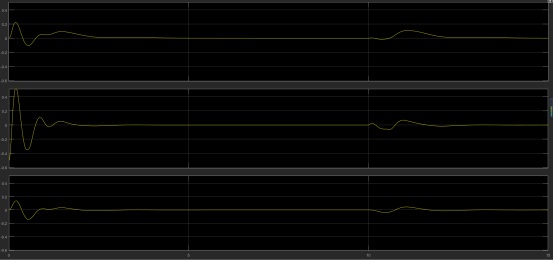
 二級倒立擺模糊控制7級.doc
(2.61 MB, 下載次數: 21)
二級倒立擺模糊控制7級.doc
(2.61 MB, 下載次數: 21)
| 歡迎光臨 (http://www.raoushi.com/bbs/) | Powered by Discuz! X3.1 |