- 通過虛擬仿真，觀察平行板電容器與加蓋導體槽內部的電場分布。
- 學習用模擬法測量靜電場的方法。
- 了解影響實驗精度的因素。
被測模型有兩個：一個用來模擬無邊緣效應的平行板電容器中的電位分布；另一個用來模擬有金屬蓋的無限長接地槽形導體內電位分布。被模擬的平行板電容器，加蓋槽形導體及它們對應的模型如圖1所示。
圖1
被測模型是在碳素導電紙上按所需的幾何形狀，尺寸制成如圖1所示的金屬“電極”。為保證各被測點位置，采用“網格板”來定位。該“網格板”是用透明塑料薄板，板上沿X、Y坐標軸每一厘米打一個小孔，這樣就形成了一個正方形網格陣。
對于復雜邊界的靜電場邊值問題，用解析法求解很困難，甚至是不可能的。在實際求解過程中，直接求出靜電場的分布或電位又很困難，其精度也難以保證。本實驗根據靜電場與恒定電流場的相似性，用碳素導電紙中形成的恒定電流場來模擬無源區域的二維靜電場，從而測出邊界比較復雜的無源區域靜電場分布。
在靜電場的無源區域中，電場強度
電位移矢量
及電位
滿足下列方程：
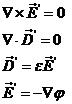\* MERGEFORMAT (1)
式中
為靜電場的介電常數。
在恒定電流場中，電場強度
、電流密度
及電位
滿足下列方程：
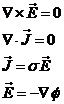\* MERGEFORMAT (2)
式中
為恒定電流場中導電媒質的電導率。
因為方程組(1)與方程組(2)在形式上完全相似，所以
（靜電場中的電位分布函數）與
（恒定電流場中的電位分布函數）應滿足同樣形式的微分方程。由方程組(1)和方程組(2)很容易求得：
\* MERGEFORMAT (3)
\* MERGEFORMAT (4)
式中
與
處于相應的位置，它們為對偶量。
若
與
在所討論區域為均勻分布（即其值與坐標無關），則方程(3)、(4)均可簡化為拉普拉斯方程：
\* MERGEFORMAT (1.5)
\* MERGEFORMAT (1.6)
電位場解的唯一定理可知：滿足相同微分方程的兩個電位場，它們具有相同的邊界電位值，因此，在保證邊界電位值不變的情況下，我們可以用恒定電流場的模型來模擬無源區域的靜電場，當靜電場中媒質為均勻媒質時，其導電媒質也應為均勻媒質，這樣測得的恒定電流場的電位分布就是被模擬的靜電場的電位分布，不需要任何改動。
Part A 虛擬仿真平行板電容器與加蓋導體槽內的電位分布
使用Matlab或其它編程語言，編寫程序，對被測模型的電位分布進行仿真。
Part A 虛擬仿真平行板電容器與加蓋導體槽內的電位分布
設兩個平行板放在
，
的環境中，導體板厚度為0.1，間距為1，長度為1，左側導體板的電位為10V，右側導體板的電位為-10V，無限遠處空間電位為0V，初始條件滿足狄利克雷條件。電位分布的仿真結果如下：
由仿真結果可以看到，導體板間的電場強度可近似看作勻強電場，電位分布也可以近似為從左向右均勻下降。
設加蓋導體槽放在，的環境中，蓋板和槽壁的厚度均為0.1，蓋板的寬度為1，導體槽的寬度為1，深度為1。初始條件為：蓋板電位10V，導體槽接地，空間無限遠處電位0V，滿足狄利克雷條件。電位分布的仿真結果如下：
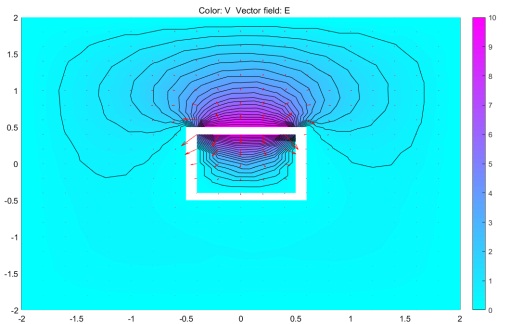
從仿真結果可以看到，等位線密度由槽底中央向槽壁和蓋板連接處逐漸變密。
附錄：
請在此處附上虛擬仿真程序代碼及其他需要附錄的文字說明或圖，可附頁。
一．
>>pdetool
1.畫兩個平行板：R1 R2和介質 R3：
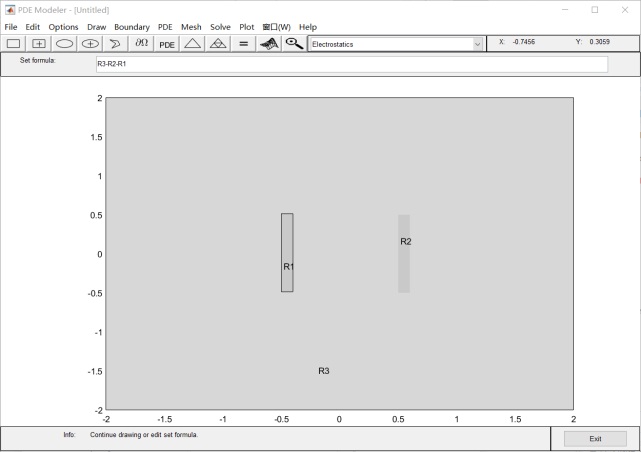
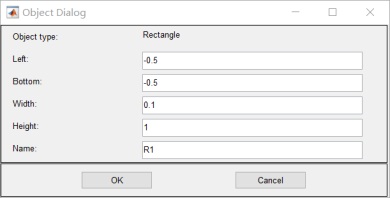
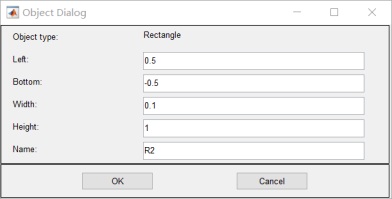
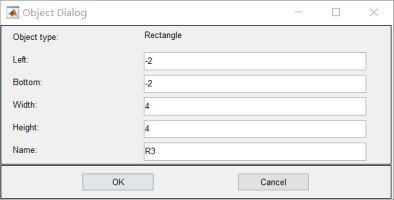
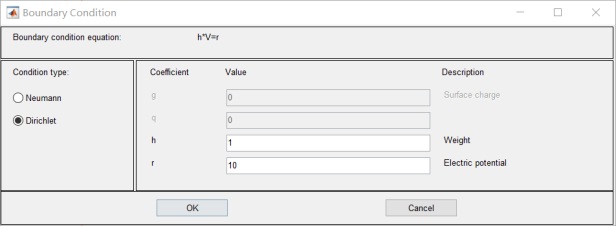
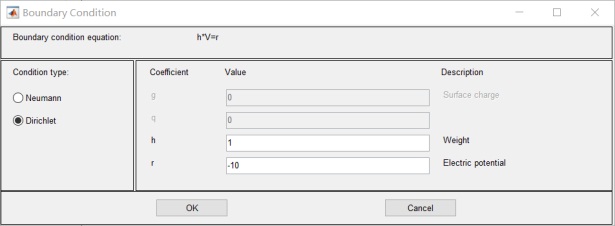
介質邊界為0，左邊電極板為10v，右面電極板為-10v:
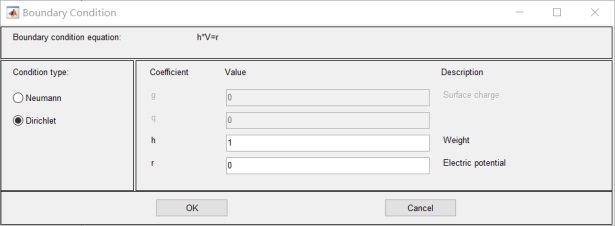
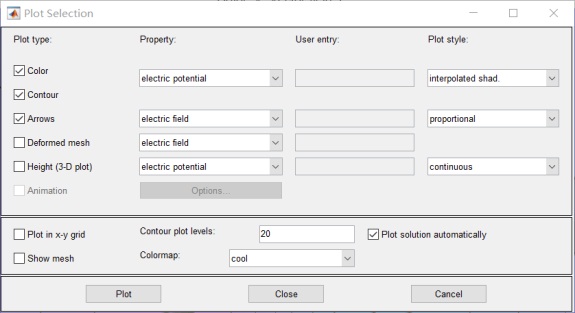
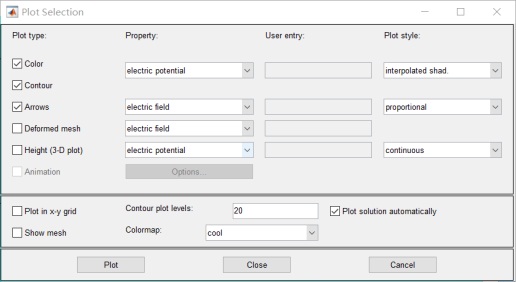
勾選contour和Arrows：
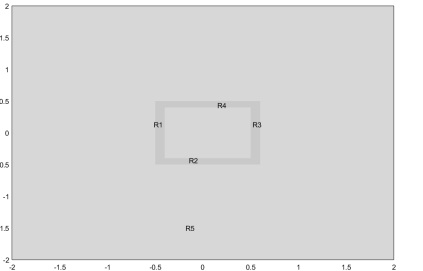
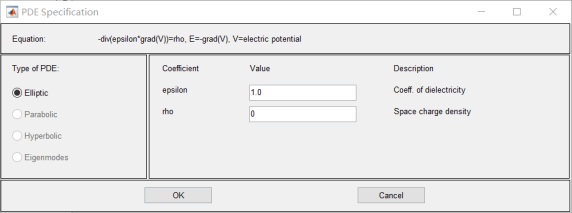
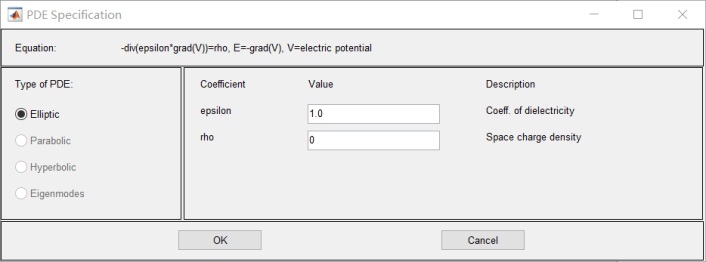
3.設置參數：
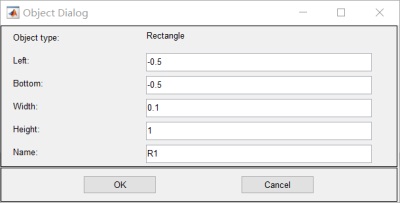
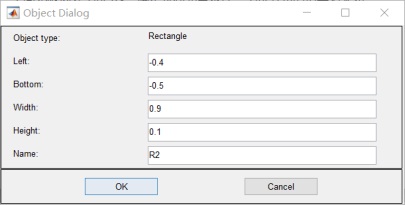
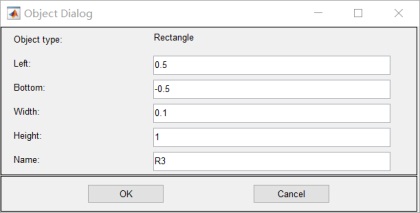
4.函數方程改為：
5. 將所求類型改為：
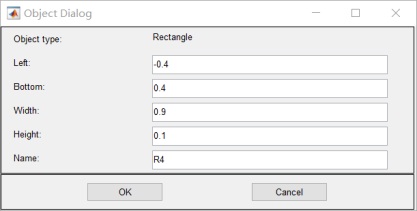
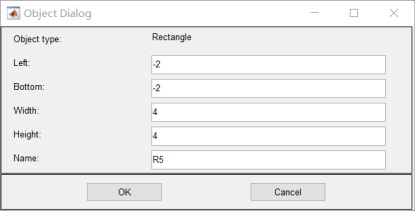
6.設置邊界值：其中R1 R2 R3 電位為0；R4 為10v 無窮遠為0v：
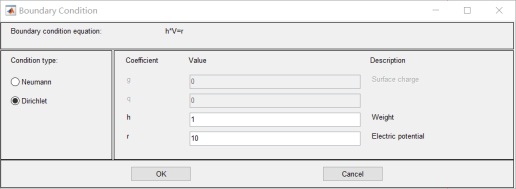
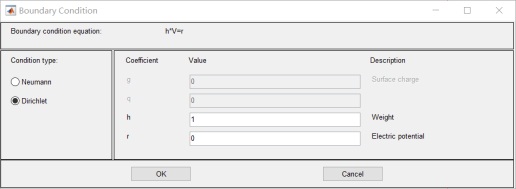
7.設置 介質參數：
8.畫圖：
完整的Word格式文檔51黑下載地址：
靜電場邊值問題研究實驗.docx
(786.33 KB, 下載次數: 3)
| 歡迎光臨 (http://www.raoushi.com/bbs/) | Powered by Discuz! X3.1 |