欧美极品高清xxxxhd,国产日产欧美最新,无码AV国产东京热AV无码,国产精品人与动性XXX,国产传媒亚洲综合一区二区,四库影院永久国产精品,毛片免费免费高清视频,福利所导航夜趣136

標(biāo)題: 四元數(shù)歐拉角解算詳細(xì)解說(shuō) [打印本頁(yè)]

作者: 哈哈2020 時(shí)間: 2019-12-25 13:53
標(biāo)題: 四元數(shù)歐拉角解算詳細(xì)解說(shuō)
四元數(shù)歐拉角解算，姿態(tài)解算中要用到的

評(píng)估一個(gè)物體在空間的姿態(tài)，一般都會(huì)想到通過(guò)該物體與參考平面的傾斜角，就是斜面與斜面之間的夾角。但是計(jì)算起來(lái)實(shí)際上我們要把這個(gè)過(guò)程分解成很多個(gè)矢量。所以解算姿態(tài)的時(shí)候可以把剛體旋轉(zhuǎn)分解成三個(gè)軸上的歐拉角
首先稍微說(shuō)一下，歐拉角就是剛體繞三個(gè)軸的旋轉(zhuǎn)角度。歐拉角與旋轉(zhuǎn)角度和旋轉(zhuǎn)軸的旋轉(zhuǎn)順序有關(guān)。但是標(biāo)準(zhǔn)上規(guī)定XYZ軸為旋轉(zhuǎn)軸順序。歐拉旋轉(zhuǎn)與外界的參考系并沒(méi)有關(guān)系。平時(shí)6050得出來(lái)的Yaw（繞Z軸）、Pitch（繞X軸）、Roll（繞Y軸）這三個(gè)是以地球作為參考系（一般以東、北、天三個(gè)方向?yàn)閰⒖汲跏键c(diǎn)），所以要區(qū)分的是歐拉角本身是以剛體本身為坐標(biāo)軸的概念。
下面介紹一下歐拉角的致命缺點(diǎn) Gimbal Lock（萬(wàn)向節(jié)死鎖）
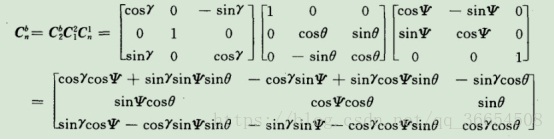
這個(gè)先用一句話囊括一下：不同的坐標(biāo)值對(duì)應(yīng)空間同一個(gè)位置，多個(gè)坐標(biāo)值對(duì)應(yīng)同一個(gè)位置的不一致性是造成死鎖的根源。
然后就舉個(gè)例子：
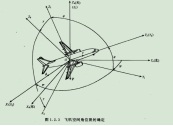
假如我們有一個(gè)望遠(yuǎn)鏡和一個(gè)用來(lái)放望遠(yuǎn)鏡的三腳架，（我們將）三腳架放在地面上，使支撐望遠(yuǎn)鏡的三腳架的頂部是平行于地平面（參考平面）的，以便使得豎向的旋轉(zhuǎn)軸（記為 x 軸）是完全地垂直于地平面的。現(xiàn)在，我們就可以將望遠(yuǎn)鏡饒 x 軸旋轉(zhuǎn) 360 度，從而觀察（以望遠(yuǎn)鏡為中心的）水平包圍圈的所有方向。通常將正北朝向方位角度記為 0 度方位角。第二個(gè)坐標(biāo)軸，即平行于地平面的橫向的坐標(biāo)軸（記為 y 軸）使得望遠(yuǎn)鏡可以饒著它上下旋轉(zhuǎn)，通常將地平面朝向的仰角記為 0 度，這樣，望遠(yuǎn)鏡可以向上仰+90 度指向天頂，或者向下-90 度指向腳底。好了，萬(wàn)事俱備。現(xiàn)在，天空中（包括地面上）的每個(gè)點(diǎn)只需要唯一的一對(duì) x 和 y 度數(shù)就可以確定。比如 x=90 度,y=45 度指向的點(diǎn)是位于正東方向的半天空上。
現(xiàn)在，看看萬(wàn)向節(jié)死鎖是怎么發(fā)生的。一次，我們探測(cè)到有一個(gè)飛行器貼地飛行，位于望遠(yuǎn)鏡的正東方向（x=90 度，y=10 度），朝著我們直飛過(guò)來(lái)，我們跟蹤它。飛行器飛行方向是保持 x 軸角度 90 度不變，而 y 向的角度在慢慢增大。隨著飛行器的臨近，y 軸角增長(zhǎng)的越來(lái)越快且當(dāng) y 向的角度達(dá)到 90 度時(shí)（即將超越），突然它急轉(zhuǎn)彎朝南飛去。這時(shí)，我們發(fā)現(xiàn)我們不能將望遠(yuǎn)鏡朝向南方，因?yàn)榇藭r(shí) y 向已經(jīng)是 90 度，造成我們失去跟蹤目標(biāo)。這就是萬(wàn)向節(jié)死鎖！
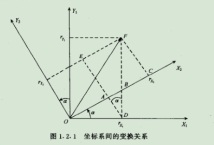
為什么說(shuō)不能將望遠(yuǎn)鏡朝向南方呢，讓我們看看坐標(biāo)變化，從開(kāi)始的（x=90 度，y=10度）到（x=90 度，y=90 度），這個(gè)過(guò)程沒(méi)有問(wèn)題，望遠(yuǎn)鏡慢慢轉(zhuǎn)動(dòng)跟蹤飛行器。當(dāng)飛行器到達(dá)（x=90 度，y=90 度）后，坐標(biāo)突然變成（x=180 度，y=90 度）（因?yàn)槌希瑇由 90突變成 180 度,所以望遠(yuǎn)鏡需要饒垂直軸向 x 軸旋轉(zhuǎn) 180-90=90 度以便追上飛行器,但此時(shí)，望遠(yuǎn)鏡已經(jīng)是平行于 x 軸，我們知道饒平行于自身的中軸線的的旋轉(zhuǎn)改變不了朝向，就象擰螺絲一樣，螺絲頭的指向不變。所以望遠(yuǎn)鏡的指向還是天頂。而后由于飛行器飛遠(yuǎn)，坐標(biāo)變成（x=180 度，y<90 度）時(shí)，y 向角減小，望遠(yuǎn)鏡只能又轉(zhuǎn)回到正東指向，望’器’興嘆。這說(shuō)明用 x,y 旋轉(zhuǎn)角（又稱歐拉角）來(lái)定向物體有時(shí)并不能按照你想像的那樣工作，象上面的例子中從（x=90 度，y=10 度）到（x=90 度，y=90 度），按照歐拉角旋轉(zhuǎn)確實(shí)可以正確地定向，但從（x=90 度，y=90 度）到（x=180 度，y=90 度），再到（x=180 度，y<90 度）,按照歐拉角旋轉(zhuǎn)后的定向并非正確。我的理解是坐標(biāo)值的變化和飛行器空間的位置變化一一對(duì)應(yīng)，但是從（x=90 度，y=90 度）到（x=180 度，y=90 度），再到（x=180 度，y<90度）這個(gè)變化，飛行器位置是連續(xù)的變化，但坐標(biāo)值的變化卻不是連續(xù)的（從 90 突變到180），其原因在于（x=90 度，y=90 度）和（x=180 度，y=90 度）甚至和（x=任意度，y=90 度）這些不同的坐標(biāo)值對(duì)應(yīng)空間同一個(gè)位置。。。
同樣對(duì)于2維或者3維都是一樣的（例子是抄的、、、）
現(xiàn)在介紹一下方向余弦，為什么類？一方面方向余弦可以表示矢量在坐標(biāo)軸中的位置，二是可以簡(jiǎn)化運(yùn)算。詳見(jiàn)下。。
剛剛說(shuō)過(guò)可以用方向余弦表示矢量在坐標(biāo)軸的位置，也就是說(shuō)可以得出載體坐標(biāo)軸xyz分別與參考坐標(biāo)軸XYZ的方向余弦。形成余弦矩陣

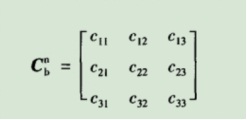
第i行、第j列的元素表示參考坐標(biāo)系i軸和載體坐標(biāo)系j軸夾角的余弦。
回過(guò)頭來(lái)再比較一下歐拉角和方向余弦其實(shí)沒(méi)有什么區(qū)別，就是用方向余弦表示歐拉角。這兩個(gè)的坐標(biāo)變換在《慣性導(dǎo)航》里面都有相應(yīng)的推導(dǎo)。（此處略）

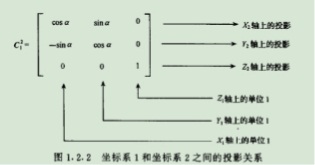
三個(gè)坐標(biāo)軸的變換用矩陣表示就是這樣

此處再說(shuō)明一下矩陣的意義。
C 表示坐標(biāo)系1到坐標(biāo)系2的變換矩陣

在線性代數(shù)中兩復(fù)雜矩陣的變化可通過(guò)有限的矩陣相乘的運(yùn)算獲得，當(dāng)然在坐標(biāo)系中同樣也適用。兩坐標(biāo)系任何復(fù)雜的角位置關(guān)系都可以看做有限次基本旋轉(zhuǎn)的組合

按上面推論，此矩陣的下面三個(gè)就是三軸對(duì)應(yīng)的方向余弦，γ、θ、ψ就是歐拉角。

不管怎么說(shuō)，要做到表示三維空間的矢量就要用到四元數(shù)。。。。原因的話就不扯了，具體可以看看百度了解一下。。。

四元數(shù)的表示方式：
下面說(shuō)一下四元數(shù)是如何表示旋轉(zhuǎn)的。。。。
這個(gè)過(guò)程可以大概給一個(gè)定義：一個(gè)單位四元數(shù)可以表示一個(gè)旋轉(zhuǎn)
大概意思就是：從一個(gè)坐標(biāo)系轉(zhuǎn)換到另一個(gè)坐標(biāo)系可以通過(guò)繞一個(gè)定義在參考坐標(biāo)系中的矢量u的單次轉(zhuǎn)動(dòng)來(lái)實(shí)現(xiàn)。

設(shè) Q = a + bi + cj +dk ，我們可以寫(xiě)成[w，v],其中 w=a，v=bi + cj +dk。那么，v 是矢量，表示三維空間里的旋轉(zhuǎn)軸。w 標(biāo)量，表示旋轉(zhuǎn)角度。所以，一個(gè)四元數(shù)可以表示一個(gè)完整的旋轉(zhuǎn)。但要注意只有單位四元數(shù)才可以表示旋轉(zhuǎn)，這個(gè)是約束條件。